Ricochet Robot
Implementation of a board game called Ricochet Robot (Rasende Roboter) including a GUI and a very fast solver.
Source Code
https://github.com/fogleman/Ricochet
Slides
https://speakerdeck.com/fogleman/ricochet-robots-solver-algorithms
Discussion
My friend introduced me to a board game called Ricochet Robot (or Rasende Roboter in its original German form). It's a fun game, but I found it even more fun as a programming problem. I implemented the game in Python, including a user interface and a solver. After that, I sped up the solver tremendously by porting it to C.
The Rules
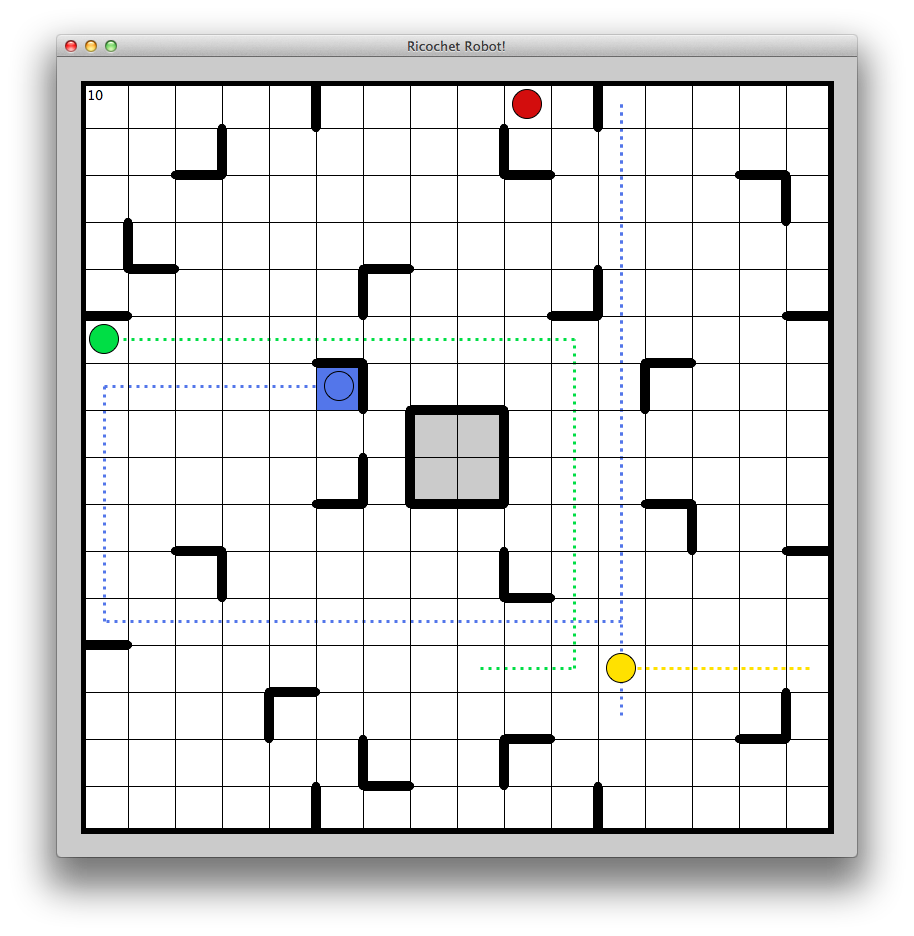
The board is a 16x16 grid. It is made up of 4 double-sided quadrants. You piece the 4 quadrants together such that the designated corner pieces line up. Since you arrange them randomly and they are double-sided, there are 96 possible board configurations. The outer perimeter is walled and there are other walls placed somewhat sparingly but methodically across the board.
There are 16 tokens on the board, 4 in each quadrant. They are color coded (red, green, blue and yellow) symbols (circle, triangle, square and hexagon) - all 16 unique combinations appear once.
Four robots (red, green, blue and yellow) are placed randomly on the board.
A random token is selected as the goal (the yellow circle, for example). The objective is to move the like-colored robot to the goal token.
The robots move like rooks in chess - in straight horizontal or vertical lines. But they must move until they hit an obstacle - walls or other robots. So moving a robot to the goal may require moving other robots around to use as obstacles.
All players view the board and look for a solution. Once a player finds a solution, they call out the number of moves required. This starts a 1-minute timer for other players to find a better solution. Once the timer expires, the player with the lowest number of moves gets to demonstrate their solution.
Or you can just play by yourself. In that sense, it's more of a puzzle than a game.
The User Interface
I implemented a simple user interface in Python using the wxPython library (it's cross platform). It shows the board, the walls, the robots, the active token, and the paths the robots have taken (as dotted lines). The number of moves is shown at the upper left.
Controls
To move a robot, first select one by color and then use the arrow keys to move it up, down, left or right.
- R - Red
- G - Green
- B - Blue
- Y - Yellow
Other controls are listed below.
- N - New Game
- S - Solve
- U - Undo
- Esc - Quit
The Algorithm
Now for the fun part!
For the solver, a brute force approach was the best I could come up with. But there are several optimizations that make this approach work quite well.
For the board representation, I used an array of 256 bytes, one for each cell in the grid. I use 5 bits for each: one for each direction to indicate walls (N, S, E, W) and one to indicate presence of a robot. Another array of 4 bytes stores the position of each robot. This representation makes move generation very quick.
A brute force, recursive search using iterative deepening is used to find an optimal solution. When searching leaf nodes, only the active robot is searched since it has to be the last robot to move in any winning solution.
The most important aspect is a hash set for memoization purposes. It allows pruning any sub-trees that have already been searched (and failed to find a solution). One hash set is used for each search depth. The keys to the hash set are the four robot positions - one byte each - hence, a 32-bit unsigned integer. If a particular position has already been searched at a certain depth, it is not searched again. This reduces the search space significantly. (The "hits" column below shows how many times a sub-tree was pruned.)
Depth: 1, Nodes: 2 (1 inner, 0 hits)
Depth: 2, Nodes: 23 (11 inner, 0 hits)
Depth: 3, Nodes: 172 (98 inner, 35 hits)
Depth: 4, Nodes: 901 (548 inner, 267 hits)
Depth: 5, Nodes: 3780 (2423 inner, 1364 hits)
Depth: 6, Nodes: 13552 (9116 inner, 5651 hits)
Depth: 7, Nodes: 42928 (29864 inner, 19570 hits)
Depth: 8, Nodes: 124465 (88827 inner, 60463 hits)
Depth: 9, Nodes: 336833 (245555 inner, 172210 hits)
Depth: 10, Nodes: 857859 (637850 inner, 458954 hits)
Depth: 11, Nodes: 2065153 (1564155 inner, 1150556 hits)
Depth: 12, Nodes: 4722920 (3638085 inner, 2726981 hits)
Depth: 13, Nodes: 10310599 (8067789 inner, 6147973 hits)
Depth: 14, Nodes: 21557884 (17124559 inner, 13246730 hits)
Depth: 15, Nodes: 43257167 (34865581 inner, 27344583 hits)
Once I had a blazing fast solver, I churned through thousands of random games and generated a histogram based on the required number of moves.
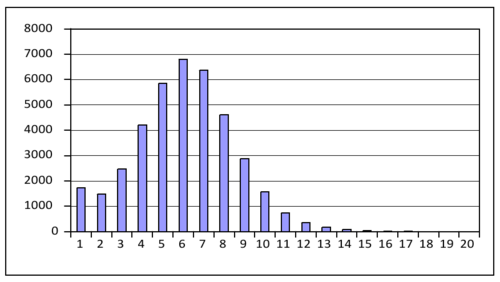
It seems that the game is always solvable - at least, I haven't found an unsolvable configuration yet. Most board configurations can be solved in under 10 moves and are solved almost immediately by the algorithm (well under one second). The hardest configuration found so far by running through millions of games is 21 moves. It takes a couple minutes to solve at that depth.
Remarks
Ricochet Robot is a cool game and makes for a fun programming project. There are a few different editions of the game and different variants - be sure to check it out!